728x90
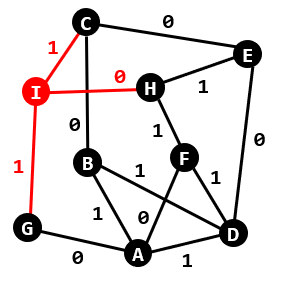
0-1 BFS란, 기존 BFS 알고리즘을 응용한 것으로 가중치가 0이나 1로만 주어진 그래프에서 최단 경로를 찾는 알고리즘이다.
최단 경로를 찾는 알고리즘으로는 다익스트라 알고리즘이 대표적이다. 그러나, 다익스트라 알고리즘으로는 O(ElogV) 또는 O(ElogE)의 시간복잡도를 갖지만 0-1 BFS 알고리즘은 O(V+E)의 시간복잡도를 가진다.
0-1 BFS 알고리즘 구현을 위해서는 덱 자료구조를 사용한다. 가중치가 낮은 간선이 우선순위가 높기 때문에 아래의 두 가지 규칙을 추가한다.
- 간선의 가중치가 0이라면 덱의 front에 정보를 추가한다.
- 간선의 가중치가 1이라면 덱의 back에 정보를 추가한다.
백준에서 풀 수 있는 대표적인 0-1 BFS 알고리즘이 적용되는 문제에는 13549번이 있다.
https://www.acmicpc.net/problem/13549
13549번: 숨바꼭질 3
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일
www.acmicpc.net
이 문제는 순간이동을 할 경우에 0초 또는 1초로 이동할 수 있으므로 0-1 BFS 알고리즘을 적용할 수 있다.
이 13549번 문제는 그래도 시간제한이 느슨한지 0-1 BFS 알고리즘 이외에 다익스트라 알고리즘으로 풀리기는 했었다.
▶ 다익스트라 알고리즘 풀이
import sys
from heapq import heappush, heappop
input = sys.stdin.readline
MAX = 100001
n, k = map(int, input().split())
dist = [int(2e9) for _ in range(MAX)]
heap = [[0, n]]
dist[n] = 0
while heap:
Time, cur = heappop(heap)
if cur*2 < MAX and dist[cur] < dist[cur*2]:
dist[cur*2] = dist[cur]
heappush(heap, [Time, cur*2])
if cur+1 < MAX and dist[cur]+1 < dist[cur+1]:
dist[cur+1] = dist[cur]+1
heappush(heap, [Time+1, cur+1])
if cur-1 >= 0 and dist[cur]+1 < dist[cur-1]:
dist[cur-1] = dist[cur]+1
heappush(heap, [Time+1, cur-1])
print(dist[k])
▶ 0-1 BFS 알고리즘 풀이
import sys
from collections import deque
input = sys.stdin.readline
MAX = 100001
n, k = map(int, input().split())
visited = [False for _ in range(MAX)]
dist = [int(2e9) for _ in range(MAX)]
q = deque([n])
visited[n] = True
dist[n] = 0
while q:
cur = q.popleft()
if cur*2 < MAX and not visited[cur*2]:
visited[cur*2] = True
q.appendleft(cur*2)
dist[cur*2] = dist[cur]
if cur+1 < MAX and not visited[cur+1]:
visited[cur+1] = True
q.append(cur+1)
dist[cur+1] = dist[cur] + 1
if cur-1 >= 0 and not visited[cur-1]:
visited[cur-1] = True
q.append(cur-1)
dist[cur-1] = dist[cur] + 1
print(dist[k])
728x90
'알고리즘' 카테고리의 다른 글
| 순환 알고리즘과 반복 알고리즘 (0) | 2023.04.10 |
|---|---|
| 알고리즘의 성능 분석(시간 복잡도, 공간 복잡도, 빅오 표기법) (0) | 2023.04.10 |
| 재귀 방법으로 순열과 조합 구현하기 (0) | 2023.02.08 |
| ★ 코딩 테스트에 나오는 알고리즘/문제 유형 총정리 (0) | 2023.02.01 |
| 6가지 대표적인 정렬 알고리즘(Sorting Algorithm) (1) | 2022.12.29 |