공대생 기록장

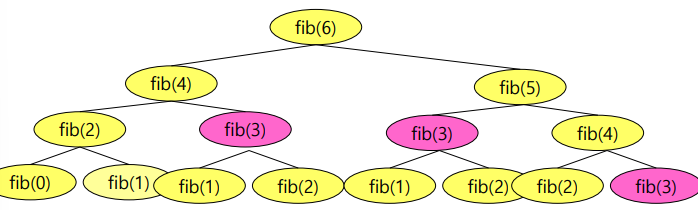
순환 알고리즘 순환 알고리즘이란 알고리즘이나 함수가 수행 도중에 자기 자신을 다시 호출하여 문제를 해결하는 기법을 말한다. 문제의 정의 자체가 순환적으로 되어 있는 경우에 적합한 방법이다. 그러나, 예로 들어 피보나치값을 계산할 때 같은 항을 중복해서 계산했던 것처럼 함수 호출의 오버헤드 문제가 발생할 수 있다. 순환 알고리즘은 순환 호출을 하는 부분과 순환 호출을 멈추는 부분으로 이루어져 있다. 반복 알고리즘 반복 알고리즘은 for나 while을 이용하여 반복한다. 수행속도가 빠르지만, 순환적인 문제에 대해서는 프로그램 작성이 어려울 수 있다. 다양한 알고리즘 1. 팩토리얼 구하기 int factorial_recur(int n) { // 순환적 방법 if (n == 1) return 1; return ..

알고리즘의 성능 분석 방법 1. 수행 시간 측정 두 개의 알고리즘의 실제 수행 시간을 측정한다. 실제로 구현하여야 하며, 동일한 하드웨어를 사용해야 한다. 2. 알고리즘의 복잡도 분석 알고리즘이 수행하는 연산의 횟수를 측정하여 비교한다. 실제로 구현하지 않아도 된다. 연산의 수행 횟수는 입력의 개수 n에 대한 함수이다. 2-1) 시간 복잡도 전체 소요 시간 = 컴파일 시간 + 실행 시간 방법: 전역 변수 count의 사용, 단계수 테이블 방식 2-2) 공간 복잡도 공간 요구량 = 고정 공간 요구 + 가변 공간 요구 고정 공간: 프로그램 입출력의 횟수나 크기와 관계없는 공간 가변 공간: 해당 문제의 인스턴스(I)에 의존하는 공간 Asymptotic Notation(점근 표기법) 점근 표기법에는 빅오(함수의..

0-1 BFS란, 기존 BFS 알고리즘을 응용한 것으로 가중치가 0이나 1로만 주어진 그래프에서 최단 경로를 찾는 알고리즘이다. 최단 경로를 찾는 알고리즘으로는 다익스트라 알고리즘이 대표적이다. 그러나, 다익스트라 알고리즘으로는 O(ElogV) 또는 O(ElogE)의 시간복잡도를 갖지만 0-1 BFS 알고리즘은 O(V+E)의 시간복잡도를 가진다. 0-1 BFS 알고리즘 구현을 위해서는 덱 자료구조를 사용한다. 가중치가 낮은 간선이 우선순위가 높기 때문에 아래의 두 가지 규칙을 추가한다. 간선의 가중치가 0이라면 덱의 front에 정보를 추가한다. 간선의 가중치가 1이라면 덱의 back에 정보를 추가한다. 백준에서 풀 수 있는 대표적인 0-1 BFS 알고리즘이 적용되는 문제에는 13549번이 있다. htt..

순열과 조합의 차이는 순서에 상관이 있는지 없는지이다. 조합에서는 순서가 없기 때문에 시작점보다 작은 위치는 다시 방문하지 않는다. 그러나, 순열은 순서가 있기 때문에 시작점보다 작은 위치 또한 방문해야 한다. 라이브러리없이 구현하는 방법은 dfs 알고리즘을 이용하는 것인데, 그 중에도 재귀를 이용하여 구현할 수 있다. 순열(permutation)이란, 서로 다른 n개 중에서 순서에 상관하여 r개를 뽑는 경우의 수이다. arr = [1, 2, 3, 4] select = [False for _ in range(4)] result = [] def dfs(cnt): if cnt == 3: print(*result) return for i in range(4): if not select[i]: select[i]..

알고리즘 구현(Implementation) 알고리즘: 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정이 어려운 알고리즘 브루트 포스(Brute Force) 알고리즘: 모든 경우의 수를 탐색하는 알고리즘 그리디(Greedy) 알고리즘: 각 단계마다 항상 최선의 선택을 하여 해에 근사한 값에 도달하는 알고리즘 다이나믹 프로그래밍(Dynamic Programming) 알고리즘: 큰 문제를 작은 문제들로 나누어 해결하고, 그 결과를 큰 문제 해결할 때 사용하는 알고리즘 재귀(Recursive) 알고리즘: 함수 내부에서 함수가 자기 자신을 다시 호출하여 작업을 수행하는 알고리즘 분할 정복(Divide and Conquer) 알고리즘: 큰 문제를 분할이 불가능할 때까지 나누고(divide) 작은 문제들을 해결한 후..

정렬이란, 자료형이 같은 데이터들의 집합을 대소관계에 따라 줄지어 나열하는 것이다. 알고리즘은 보다 효율적인 데이터 관리를 하는 것이 목적이다. 정렬은 그러한 알고리즘의 목적 달성을 돕는 가장 기본적이고 중요한 알고리즘이다. 데이터 탐색의 대표적인 방법에는 선형검색과 이분검색이 있는데, 이 중 이분검색을 위해서는 사전에 데이터 집합의 정렬이 반드시 필요하다. 정렬 알고리즘의 개요 1. 내부 정렬과 외부 정렬 - 내부 정렬: 정렬한 자료를 주기억장치에 저장된 상태에서 정렬 - 외부 정렬: 외부 기억장치(하드 디스크)에 대부분의 데이터가 있고, 그 중 일부만 주기억장치에 저장된 상태에서 정렬 2. 정렬 알고리즘의 종류 - 단순하지만 비효율적: 버블 정렬(Bubble sort), 선택 정렬(Selection ..

def change_toBin(n): binary = '' while n > 0: n, mod = divmod(n, 2) binary += str(mod) return binary[::-1] 언제 다 외우지..

약수 구하기 알고리즘 1. 1~자연수 n의 제곱근 중 n과 나누어떨어지는 개수 구하기 - 단, n의 제곱근의 제곱이 n인 것은 포함하지 않는다. 2. 해당 개수 * 2 3. 만약, n의 제곱근의 제곱이 n인 것이 있다면 개수에 1을 더한다. cnt = 0 for i in range(1, n + 1): if i * i >= n: cnt *= 2 if i * i == n: cnt += 1 break if n % i == 0: cnt += 1 print(cnt) # 자연수 n의 약수의 개수 OR data = [0] + [1] * e for i in range(2, e + 1): for j in range(i, e + 1, i): data[j] += 1 소수 확인 알고리즘 1. 자연수 n은 2이상이어야 한다. ..

유클리드 호제법 2개의 자연수 a, b(a > b)에 대해서 a를 b로 나눈 나머지가 r일 때, a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 시간복잡도: O(logN) > int gcd(int num1, int num2) { if (num2 == 0) return num1; else return gcd(num2, num1 % num2); } def gcd(a, b): while b > 0: a, b = b, a % b return a > cout