정렬이란, 자료형이 같은 데이터들의 집합을 대소관계에 따라 줄지어 나열하는 것이다.
알고리즘은 보다 효율적인 데이터 관리를 하는 것이 목적이다.
정렬은 그러한 알고리즘의 목적 달성을 돕는 가장 기본적이고 중요한 알고리즘이다.
데이터 탐색의 대표적인 방법에는 선형검색과 이분검색이 있는데, 이 중 이분검색을 위해서는 사전에 데이터 집합의 정렬이 반드시 필요하다.
정렬 알고리즘의 개요
1. 내부 정렬과 외부 정렬
- 내부 정렬: 정렬한 자료를 주기억장치에 저장된 상태에서 정렬
- 외부 정렬: 외부 기억장치(하드 디스크)에 대부분의 데이터가 있고, 그 중 일부만 주기억장치에 저장된 상태에서 정렬
2. 정렬 알고리즘의 종류
- 단순하지만 비효율적: 버블 정렬(Bubble sort), 선택 정렬(Selection sort), 삽입 정렬(Insertion sort)
- 복잡하지만 효율적: 퀵 정렬(Quick sort) , 병합 정렬(Merge sort), 힙 정렬(Heap sort), 셀 정렬(Shell sort), 기수 정렬(Radix sort) 등
3. 내부 정렬의 정렬 방식에 따른 구분
1) 교환 방식: 버블 정렬, 퀵 정렬
2) 선택 방식: 선택 정렬, 힙 정렬
3) 삽입 방식: 삽입 정렬, 셀 정렬
4) 병합 방식: 병합 정렬
5) 분배 방식: 기수 정렬
.4. 알아둘 것
- 모든 경우에 대하여 최적인 정렬 알고리즘은 존재하지 않는다. 상황에 따라 그때마다 적합한 알고리즘을 선택해야 한다.
- 동일한 키 값을 갖는 레코드들의 상대적인 위치는 정렬 후에도 바뀌지 않는다(안정성)

대표적인 정렬 알고리즘
1. 버블 정렬(Bubble Sort)
버블 정렬은 집합의 가장 첫 번째 원소부터 연속된 원소들끼리 크기를 비교하며 자리를 교환하는 과정을 계속해서 진행하는 방법이다. 가장 손쉽게 구현할 수 있고 직관적이지만, 알고리즘적 관점에서는 꽤나 비효율적인 정렬 방식이다.
최선의 경우: O(n^2), 평균적인 경우: O(n^2), 최악의 경우: O(n^2)

void bubble_sort() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n-1-i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
2. 선택 정렬(Selection Sort)
선택 정렬은 가장 첫 번째 원소부터 선택해서, 해당 원소의 오른쪽에 있는 원소들 중 가장 크기가 작은 원소와 자리를 교환하는 과정을 순차적으로 진행하는 방법이다. 구현이 간단하고, 비교하는 횟수에 비해 교환이 적다는 장점이 있다.
최선의 경우: O(n^2), 평균적인 경우: O(n^2), 최악의 경우: O(n^2)

void selection_sort() {
for (int i = 0; i < n - 1; i++) {
int min = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[min])
min = j;
}
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
3. 삽입 정렬(Insertion Sort)
삽입 정렬은 가장 첫 번째 원소부터 선택해서, 해당 원소의 왼쪽에 있는 모든 원소들과 비교하며 적절한 위치에 끼워넣는 과정을 순차적으로 진행하는 방법이다. 자료구조에 따라선 뒤로 밀어내는데 걸리는 시간이 크지만, 이미 정렬되어 있는 집합에 원소를 하나씩 삽입/제거하는 경우나 배열의 크기가 작을 경우에는 가장 성능이 좋은 정렬 방법이다.
최선의 경우: O(n), 평균적인 경우: O(n^2), 최악의 경우: O(n^2)

void insertion_sort() {
for (int i = 1; i < n; i++) {
for (int j = i; j > 0; j--) {
if (arr[j - 1] > arr[j]) {
int tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
}
else break;
}
}
}
5. 퀵 정렬(Quick sort)
퀵 정렬은 pivot poing(피벗) 이라는 포인트를 하나 설정하고, 이 값을 기준으로 작은 값을 왼쪽, 큰 값은 오른쪽으로 옮기는 방법으로 정렬을 진행한다. 해당 과정을 반복하여 분할된 배열의 크기가 1이 되면 배열의 정렬이 완료된다. 병합 정렬과 마찬가지로 분할 정복(Divide and conquer) 방식을 이용하였다.
최선의 경우: O(nlogn), 평균적인 경우: O(nlogn), 최악의 경우: O(n^2)
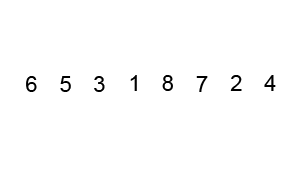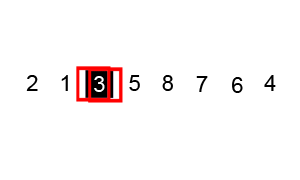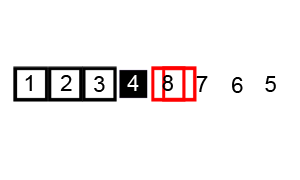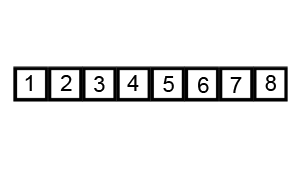
4. 합병 정렬/병합 정렬(Merge sort)
합병 정렬/병합 정렬은 분할 정복(Divide and conquer) 방식으로 설계된 알고리즘이다. 폰 노이만이 개발했으며, 큰 문제를 반으로 쪼개고 이후 다시 병합함으로써 문제를 해결하는 방법으로, 분할 과정은 배열의 크기가 1보다 같거나 작을 때까지 반복한다. 계속해서 배열을 쪼개 나간 뒤, 모든 배열을 합쳐서 정렬된 하나의 배열을 출력한다.
최선의 경우: O(nlogn), 평균적인 경우: O(nlogn), 최악의 경우: O(nlogn)
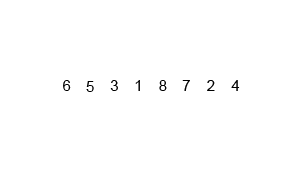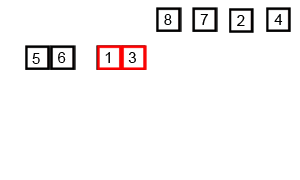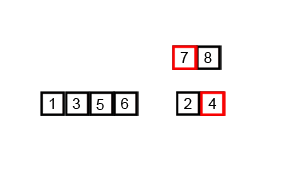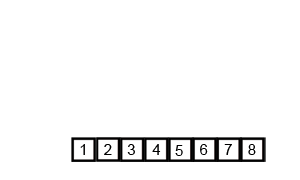
def merge(arr, left, mid, right):
i, j = left, mid+1
res = []
while i <= mid and j <= right:
if arr[i] <= arr[j]:
res.append(arr[i])
i += 1
else:
res.append(arr[j])
j += 1
while i <= mid:
res.append(arr[i])
i += 1
while j <= right:
res.append(arr[j])
j += 1
for idx in range(left, right+1):
arr[idx] = res[idx-left]
return arr
def merge_sort(arr, left, right):
if left < right:
mid = (left + right) // 2
merge_sort(arr, left, mid)
merge_sort(arr, mid+1, right)
merge(arr, left, mid, right)
6. 힙 정렬(Heap sort)
힙 정렬은 최대 힙 트리나 최소 힙 트리를 이용하여 정렬을 하는 방법으로, 내림차순 정렬을 위해서는 최대 힙을 이용하고, 오름차순 정렬을 위해서는 최소 힙을 이용한다.
'알고리즘' 카테고리의 다른 글
| 재귀 방법으로 순열과 조합 구현하기 (0) | 2023.02.08 |
|---|---|
| ★ 코딩 테스트에 나오는 알고리즘/문제 유형 총정리 (0) | 2023.02.01 |
| 10진수를 2진수로 - 파이썬 (0) | 2022.12.22 |
| 약수 개수 구하기 / 소수 확인 알고리즘 (0) | 2022.11.20 |
| 최대공약수, 최소공배수 알고리즘 (0) | 2022.11.12 |