배열(ArrayList)

배열은 <인덱스, 요소> 쌍의 집합으로, 같은형의 변수를 여러 개 담을 수 있는 자료구조이다. 1차원 배열과 2차원 배열 등 여러 차원이 존재할 수 있다.
한 번 선언된 배열의 정적인 메모리 크기로 인한 문제를 해결하기 위해 동적 배열이 등장하였다. 동적 배열의 원리는 데이터가 추가되면서 메모리가 꽉 차면 메모리의 크기를 보통 2배를 늘려주고 데이터들을 모두 복사하는 방법으로, 이를 더블링(Doubling)이라고 한다.
특징
- 인덱스를 이용하므로 배열 내 요소의 탐색은 O(1)의 시간복잡도를 가진다.
- 배열의 데이터의 삽입과 삭제 시 데이터의 이동이 빈번하게 발생한다.
- 데이터의 삽입과 삭제에서의 시간복잡도는 최선의 경우 O(1), 최악의 경우 O(n)을 가진다.
- 고정된 크기의 저장공간이므로 할당된 크기보다 적게 사용할 때 비효율적이다.
- 메모리 상의 연속된 블록에 저장되므로 연결 리스트보다 공간 복잡도가 좋다.
연결 리스트(LinkedList)

연결 리스트는 각 노드가 데이터 필드와 포인터가 있는 링크 필드를 가지고 다음 데이터를 가리키는 방식으로 데이터를 저장하는 자료구조이다. 기본적으로 삽입, 삭제, 탐색 연산이 존재하며 배열 또는 연결 리스트를 이용하여 구현할 수 있다. 종류로는 단일 연결 리스트(Singly Linked List), 이중 연결 리스트(Doubly Linked LIst), 원형 연결 리스트(Circular Linked List)가 있다.
특징
- 탐색을 가장 첫 번째 노드부터 시작하므로 최악의 경우에는 O(n)의 시간복잡도를 가진다.
- 데이터 추가 또는 삭제의 과정이 O(1)로 빠르다.
- 동적으로 메모리를 사용할 수 있어 효율적이다.
High Level
Q. 전제 조건(precondition)이 만족되지 않았어도 사후 조건(postcondition)이 만족될 수도 있는가?
=> X / 전제 조건이 만족되지 않았다면 코드를 수행하지 못했을 것이므로 사후 조건이 확인될 일이 없다.
Q. 2차원 행렬을 1차원 배열로 표현할 때 같은 행에 있는 요소부터 근접한 공간에 저장하는 것을 ___라 한다.
=> Row-major order / row-major order은 말 그대로 하나의 row를 완전히 저장하고 다음 row를 저장하는 행렬 저장방식이다. 따라서, 아래 그림과 같이 행렬을 읽고, 메모리에 아래와 같이 1차원 배열 형태로 저장한다.
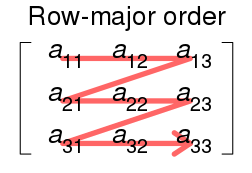
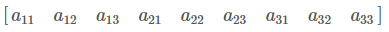
Q. 4x4 2차원 행렬을 column-major order로 저장했을 때 (row, column)이 (2,1)인 요소의 인덱스는?
=> 1 / column-major order는 같은 열인 요소들부터 근접한 위치에 저장하므로, 첫 요소인 (1,1)이 0번 인덱스에 저장되는 것을 시작으로 (2,1)가 1번, (3,1)이 2번 인덱스가 된다.
Q. 하노이의 탑(Tower of Hanoi) 문제에서 n개의 원판을 옮기는 데 최소 몇 번의 이동이 필요한가?
=> 2^n - 1 / 수학적 귀납법을 통해 증명할 수 있으며, 2^n - 1은 메르센 수(Mersenne number)라고도 불린다.
Q. 기수 정렬(radix sort)과 이진 탐색(binary search) 중 연결 리스트를 사용하여 더 구현하기 어려운 것은?
=> 이진 탐색(binary search) / 기수 정렬은 random access가 필요없는, 즉 어떤 위치에라도 곧바로 접근할 필요가 없지만 이진 탐색은 인덱스들을 건너뛰기 위해 곧바로 접근할 필요가 있다.
Q. 배열과 Linked List 중 sparse matrix를 저장공간 최적화하여 저장하기에 적합한 자료구조는?
=> Linked List / 희소 행렬(sparse matrix)은 행렬의 값이 대부분 0인 행렬을 말한다. 행렬 안에서 값이 있는 요소의 수가 적기 때문에 행렬의 크기에 해당하는 모든 공간을 확보하지 않고, 값이 있는 요소만큼만 저장할 수 있는 Linked List가 저장공간 최적화에 배열보다 좋다.
'자료구조' 카테고리의 다른 글
| 세그먼트 트리(Segment Tree) 자료구조 (0) | 2023.02.04 |
|---|---|
| 그래프(Graph) (0) | 2022.12.30 |
| 해시 테이블(HashTable) (0) | 2022.12.30 |
| 트리(Tree)와 힙(Heap) (0) | 2022.12.30 |
| 스택(Stack)과 큐(Queue) (0) | 2022.12.29 |